【第9回】チャート形状の認識
March 30, 2021
株価サーバー テクニカル分析 python無一物中Project記事一覧
- 【第1回】株価サーバーの構築の概要
- 【第2回】無尽蔵から株価データの一括取得
- 【第3回】無尽蔵株価データから銘柄毎の時系列データを生成
- 【第4回】無尽蔵から自動で株価データを取得し株価データベースを更新
- 【第5回】出来ず株価の補填と株式分割を自動調整してチャート表示
- 【第6回】mplfinanceを使用してテクニカルチャート表示
- 【第7回】テクニカル指標による銘柄スクリーニング
- 【第8回】株価チャート配信サーバー
- 【第9回】チャート形状の認識(本記事)
はじめに
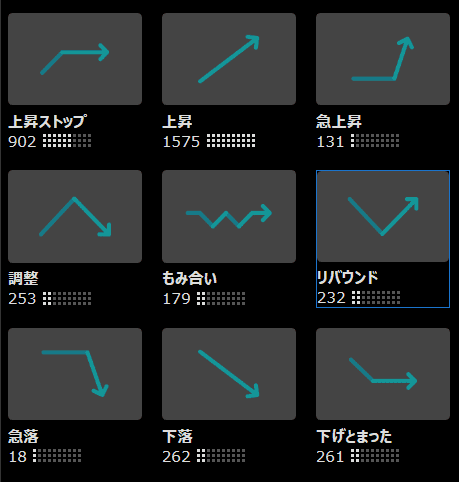
筆者が利用する楽天証券のトレーディングツール「MARKET SPEED II」には、チャート形状検索の機能があります。これは、
- 上昇ストップ
- 上昇
- 急上昇
- 調整
- もみ合い
- リバウンド
- 急落
- 下落
- 下げ止まり
のチャートの形状を認識し、該当する銘柄を教えてくれる機能です。
なかなか便利な機能なのですが、これをどうやって実現しているのだろうと気になって、自分でも試してみることにしました。これを自前で用意できれば、この機能とテクニカル分析を組み合わせて、強力なスクリーニングができるのではないかと思った訳です。
実際の投資に役立ちそうな形状は、筆者の場合「下げ止まり」、「リバウンド」あたりかな。「下げ止まり」、「リバウンド」銘柄をウォッチリストに入れて、重点監視するとか。
「急上昇」は最重要なのだけど、「MARKET SPEED II」でも、今回紹介する抽出方法でも、けっこう遅れて抽出されるので、あまり役に立ちません。
チャート形状認識実験
「MARKET SPEED II」のチャート形状認識アルゴリズムは非公開なので、知る由はありませんが、けっこうあやしい結果が得られる場合もあり、そんなにたいそうなことはやってないんじゃないかな。AIで形状を学習してとかも真っ先に思いついたのですが、もっとシンプルに、「データ同士がどの程度似ているか」を定量的にあらわしている正規化相関を利用してやってみることにします。
以下のコードでは、データ列aとb、データ列aとcの相関係数を計算しています。
import numpy as np
a = [10, 11, 12, 13, 14]
b = [10, 12, 11, 11, 12]
c = [6, 9, -8, 0, 1]
corr1 = np.corrcoef(a, b)
print(corr1[1,0])
corr2 = np.corrcoef(a, c)
print(corr2[1,0])相関係数の値は-1.0~1.0の間の値をとり、この値が1.0に近いほど似ていることを意味します。 コードの実行結果は、aとbの相関係数は0.5669467095138409、aとcの相関係数は-0.46190580640999945だから、cよりもbのほうが、aに似ているということになります。
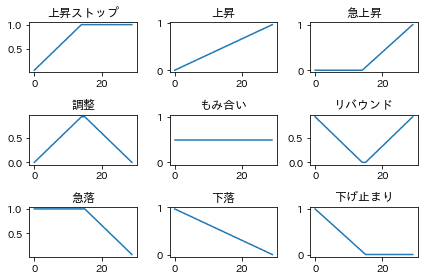
そこで、次の図のような形状毎のデータ列(形状テンプレート)を用意し、株価のデータとの相関係数を算出し、相関係数の値が1.0に近ければ、その形状であると判定します。
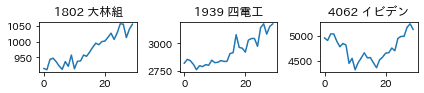
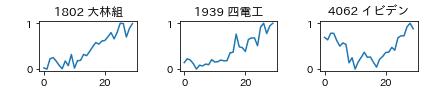
データの期間は30日間とします。例として2021/3/27時点での以下の3銘柄で試してみます。
株価が異なっても比較できるように期間の株価を0~1で正規化します。
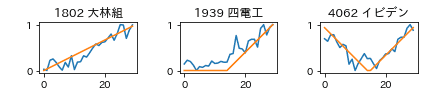
形状テンプレートと株価の相関係数と形状の判定結果は以下のようになりました。
| 1802 大林組 | 相関係数 | 判定結果 |
|---|---|---|
| 上昇ストップ | 0.7396801593636323 | |
| 上昇 | 0.9302408236379394 | ○ |
| 急上昇 | 0.9169569543912299 | |
| 調整 | -0.17099452448064192 | |
| もみ合い | 0.23862822925360594 | |
| リバウンド | 0.17099452448064195 | |
| 急落 | -0.8987018370356069 | |
| 下落 | -0.9302408236379393 | |
| 下げ止まり | -0.7701760966773804 |
| 1939 四電工 | 相関係数 | 判定結果 |
|---|---|---|
| 上昇ストップ | 0.6610759242186979 | |
| 上昇 | 0.8931602044435897 | |
| 急上昇 | 0.9257444402842008 | ○ |
| 調整 | -0.2694073532155971 | |
| もみ合い | 0.1571958709317137 | |
| リバウンド | 0.2694073532155971 | |
| 急落 | -0.9116196735909801 | |
| 下落 | -0.8931602044435897 | |
| 下げ止まり | -0.6944864950399954 |
| 4062 イビデン | 相関係数 | 判定結果 |
|---|---|---|
| 上昇ストップ | -0.24637125495374249 | |
| 上昇 | 0.17806110554600332 | |
| 急上昇 | 0.5336115201980216 | |
| 調整 | -0.8729393226699412 | |
| もみ合い | -0.15475023299510088 | |
| リバウンド | 0.8729393226699412 | ○ |
| 急落 | -0.5654458252623342 | |
| 下落 | -0.1780611055460032 | |
| 下げ止まり | 0.21571529539920017 |
- 「1802 大林組」は、「上昇」
- 「1939 四電工」は、「急上昇」
- 「4062 イビデン」は、「リバウンド」
という判定結果になりました。
そこそこいいかんじ。
全銘柄での抽出例
2021/3/26の全銘柄で、相関係数≧0.85 で形状抽出した結果は、以下の通りでした。
- 上昇ストップ 57件
- 上昇 345件
- 急上昇 604件
- 調整 0件
- もみ合い 4件
- リバウンド 94件
- 急落 10件
- 下落 34件
- 下げ止まり 196件
よくよく考えてみると、「もみ合い」を相関係数で判断するのはふさわしくない(そもそも全データが同じ価だと相関係数は算出不能)ので、「もみ合い」は、期間中の株価の標準偏差が十分小さいかで判定するように変えました。すなわち、
期間中の株価の標準偏差/期間中の株価の平均値<0.01 ならば「もみ合い」として抽出する。
また、上昇や下落でも期間の始めと終わりで10%以上価格差がある場合のみ抽出対象としました。
「調整」が0件というのは精査が必要。
これらの変更を加えた、2021/3/26の全銘柄での結果は、以下の通りでした。
- 上昇ストップ 41件
- 上昇 234件
- 急上昇 322件
- 調整 0件
- もみ合い 106件
- リバウンド 69件
- 急落 6件
- 下落 21件
- 下げ止まり 111件
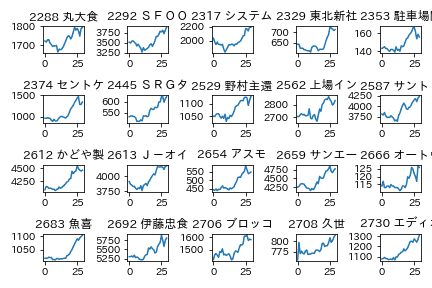
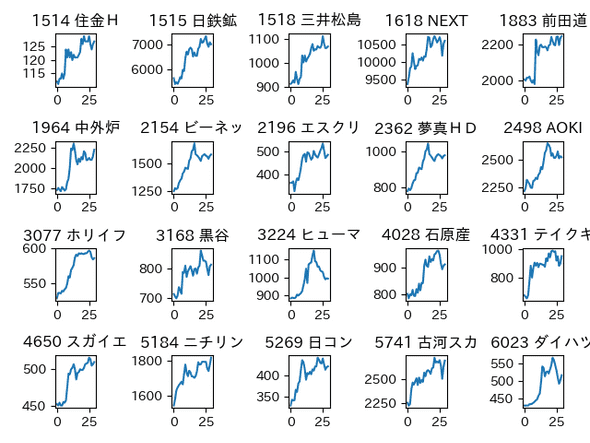
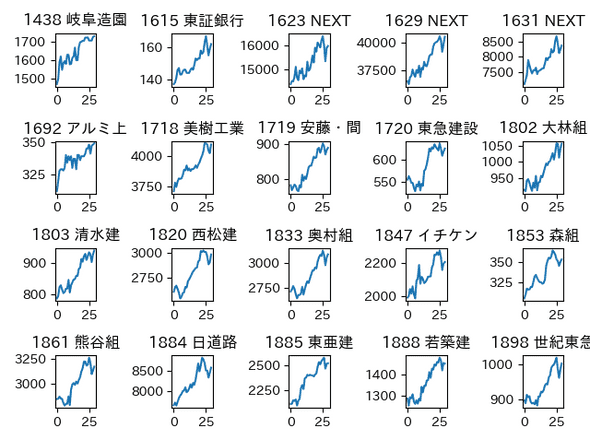
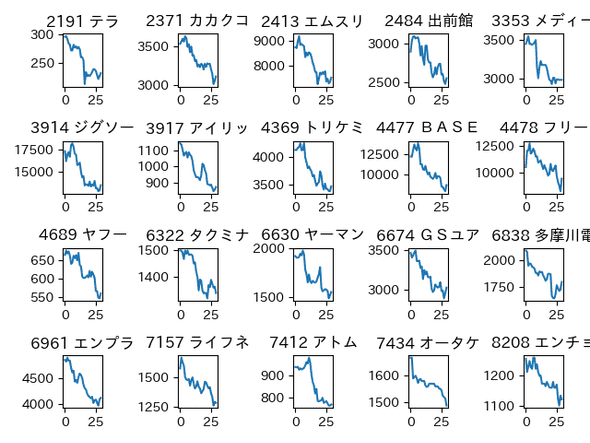
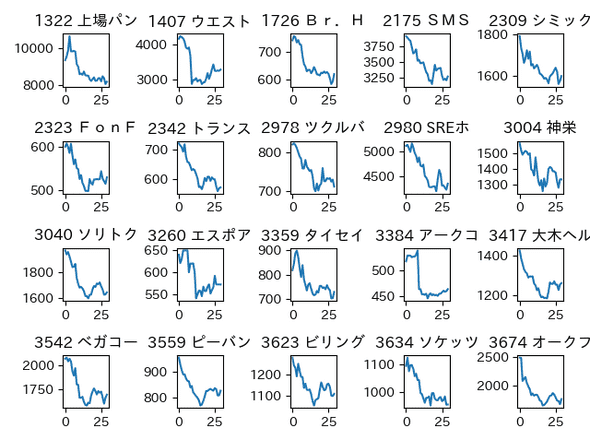
以下は抽出結果の一部です。
上昇ストップ
上昇
急上昇
もみ合い
リバウンド
急落
下落
下げ止まり
チャート形状認識の実装例
以下のcsvファイルを使って、相関係数算出のテストコードを実装してみます。
2021/02/10,906,915,905,914,2677000000
2021/02/12,910,914,902,910,3371500000
2021/02/15,926,944,924,943,3315900000
2021/02/16,955,959,942,947,2673800000
2021/02/17,946,948,935,936,2365200000
2021/02/18,939,948,920,922,2997000000
2021/02/19,915,919,909,911,2833900000
2021/02/22,932,943,931,936,3182100000
2021/02/24,929,937,921,921,3191300000
2021/02/25,950,963,943,957,3063000000
2021/02/26,950,952,909,913,5239900000
2021/03/01,924,942,924,937,1922500000
2021/03/02,941,947,929,938,2153100000
2021/03/03,936,957,936,957,2786100000
2021/03/04,957,964,942,953,2482400000
2021/03/05,965,967,946,967,2417800000
2021/03/08,984,1003,975,982,3167600000
2021/03/09,997,999,979,995,2824800000
2021/03/10,968,995,968,990,3594900000
2021/03/11,999,1014,994,1000,2865800000
2021/03/12,1007,1008,996,1002,3294000000
2021/03/15,1005,1016,1004,1014,2113000000
2021/03/16,1012,1035,1008,1027,2581500000
2021/03/17,1010,1012,997,1007,3222500000
2021/03/18,1016,1037,1014,1028,3015600000
2021/03/22,1044,1062,1039,1057,2573700000
2021/03/23,1053,1068,1049,1056,2476700000
2021/03/24,1045,1046,1011,1013,3031600000
2021/03/25,1031,1052,1028,1040,2509100000
2021/03/26,1059,1066,1050,1056,2274600000サンプルなので、形状テンプレートは、「上昇」と「急上昇」の2つしか用意していません。normalize_close_value()でpandasで読み込んだ株価データを0~1で正規化します。これをcalc_corr_coeff()により、形状テンプレートとの相関係数を算出しています。
# -*- coding: utf-8 -*-
import numpy as np
import pandas as pd
def full_up_shape(term):
# 上昇
up = range(0, term)
normalized = list(map(lambda v: v/float(term), up))
return normalized
def flat_up_shape(term):
# 急上昇
half = int(term/2)
flat = [0]*half
up = range(1, half+1)
flat[len(flat):len(flat)] = up
return list(map(lambda v: v/float(half), flat))
def normalize_close_value(df):
close_value = df['Close'].to_list()
min_value = min(close_value)
max_value = max(close_value)
return list(map(lambda v: (v-min_value)/(max_value-min_value), close_value))
def calc_corr_coeff(v1, v2):
corr = np.corrcoef(v1, v2)
return corr[1, 0]
def main():
term = 30
path = '1802.csv'
df = pd.read_csv(path, header=None,
names=['Date','Open','High','Low','Close','Volume'], encoding='UTF-8')
df['Date'] = pd.to_datetime(df['Date'])
df = df.set_index("Date")
df = df.tail(term)
close_value = normalize_close_value(df)
f_full_up = full_up_shape(term)
corr1 = calc_corr_coeff(close_value, f_full_up)
f_flat_up = flat_up_shape(term)
corr2 = calc_corr_coeff(close_value, f_flat_up)
print(corr1, corr2)
if __name__ == '__main__':
main()実行結果は、
0.9302408236379394 0.9169569543912299となるはずです。
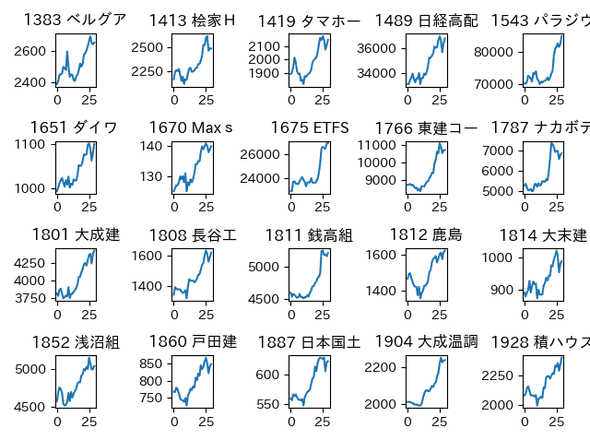
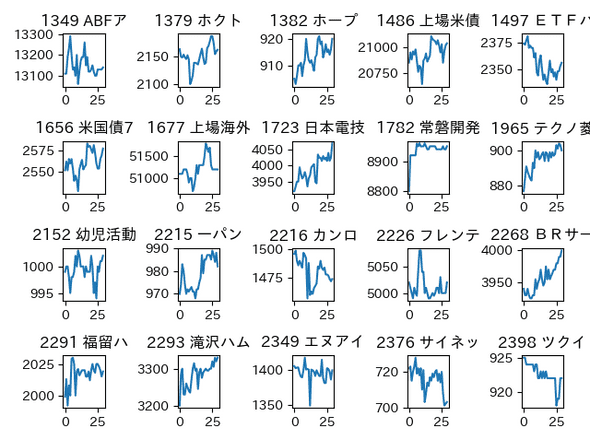
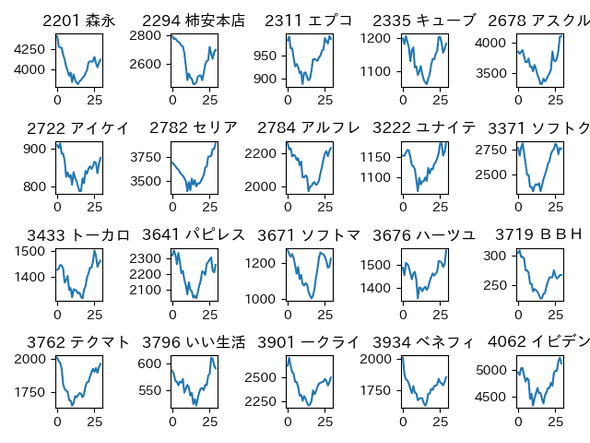
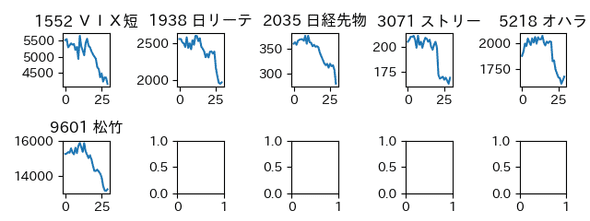
サムネイルチャート表示
本記事中では、複数のチャートをまとめてサムネイル表示させていますが、この方法を紹介しておきます。
株価データのcsvファイルが、以下のようなディレクトリに格納させているものとします。
data/ ※6
1000/
1001.csv
...
2000/
...
9000/
9001.csv
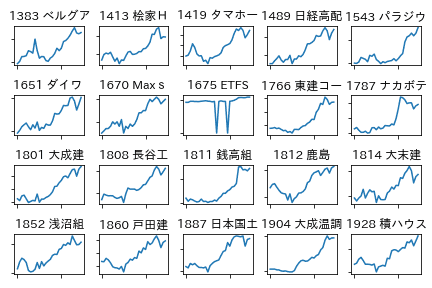
...以下のような銘柄リストをあらわすテキストファイルを読み込み、そのサムネイルを作成します。
1383,ベルグアース
1413,桧家H
1419,タマホーム
1489,日経高配指数
1543,パラジウム信託
1651,ダイワ 高配40
1670,Maxsp三菱
1675,ETFSパラジ
1766,東建コーポ
1787,ナカボテック
1801,大成建
1808,長谷工
1811,銭高組
1812,鹿島
1814,大末建
1852,浅沼組
1860,戸田建
1887,日本国土開発
1904,大成温調
1928,積ハウス
...matplotlibのsubplots()により、複数チャートを描画しています。 ただし、以下のコードでは、株価のcsvファイル中に、出来ずの場合の株価が0円となっている場合や、株式分割による不連続などは考慮されていません。
# -*- coding: utf-8 -*-
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
DATA_PATH = "../data/"
def get_close_value(df):
close_value = df['Close'].to_list()
return close_value
def read_csv(code, term):
code_dir = code[0]+"000"
path = DATA_PATH + code_dir + "/" + code + ".csv"
df = pd.read_csv(path, header=None,
names=['Date','Open','High','Low','Close','Volume'], encoding='UTF-8')
df['Date'] = pd.to_datetime(df['Date'])
df = df.set_index("Date")
df = df.tail(term)
return df
def visualize(term, codes, names):
x = np.array(list(range(0, term)))
pages = int(len(codes)/20)
if len(codes)%20 != 0: pages = pages + 1
ncols = 5
nrows = 4
i = 0
for page in range(0, pages):
fig, axes = plt.subplots(
nrows=nrows, ncols=ncols, sharex=False)
for j in range(0, ncols):
for k in range(0, nrows):
axes[k,j].tick_params(labelbottom=False,
labelleft=False,
labelright=False,
labeltop=False)
for j in range(0, nrows*ncols):
if i>=len(codes): break
df = read_csv(str(codes[i]), term)
close_value = get_close_value(df)
row = j // ncols
col = j % ncols
title =str(codes[i])+' '+names[i][:4]
axes[row,col].plot(x, np.array(close_value))
axes[row,col].set_title(title)
i = i + 1
fig.tight_layout()
filename = 'chart_thumbs'+str(page)+'.png'
plt.savefig(filename)
def main():
term = 30
filename = 'list.txt'
df = pd.read_csv(filename, header=None,
names=['code','name'], encoding='UTF-8')
codes = df['code'].to_list()
names = df['name'].to_list()
if len(codes)>0:
visualize(term, codes, names)
if __name__ == '__main__':
main()実行結果
まとめ
無一物中Project第9回では、チャートの形状を認識させる方法を紹介しました。形状テンプレートとの正規化相関で判定するだけで、それなりに使える結果が得られました。